The Centrifuge Problem
A while ago (almost 3 years ago, to be more exact) I watched a video on Numberphile where Dr Holly Krieger presents the following problem.
Given a centrifuge with \(n\) holes, is it possible to balance \(k\) test tubes?
Mathematical solution
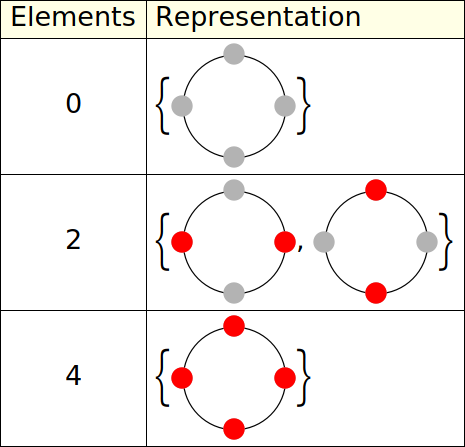
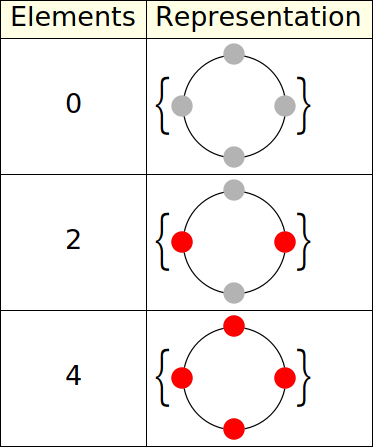
On the video Dr Krieger goes over her thinking process, and some of the intuitive (and not so intuitive) ways of constructing solutions. Particularly, a solution is valid if and only if both the number of test tubes, \(k\), and the number of empty spots, \(n - k\), can be expressed as sums of prime factors of \(n\).
The main takeaway, for me, is this problem can be thought of as finding the subset \(S\), of the set \(R\) of roots of a complex number \(z\), such that their sum is zero:
where \((\eta\omega^{j})^{n} = z\), \(\forall j \in \left\{ 0, 1, 2, \dots, n - 1 \right\}\), \(k \leq n \in \mathbb{Z}\), and \(z \in \mathbb{C}\).
For simplicity, if we take \(z = 1\), then the roots become of the form {\(1\), \(\omega\), \(\omega^{2}\), ..., \(\omega^{n-1}\)}, with \(\omega = e^{\frac{2\pi i}{n}}\). This is illustrated for \(n = 5\) in the figure below.
Finding roots of unity (\(z = 1\)) and checking subsets that add up to zero is fairly simple computational problem to solve if we brute force it, which is exactly what I did.
Computational solution
As an exercise to refresh my Mathematica programming and graphing skills, I decided to solve this problem using Wolfram Mathematica.
The problem, from a computational point of view, can be divided into main the following problems:
- Find the set of roots, \(R\).
- Find all possible subsets \(S \subseteq R\).
- Check which subsets are valid solutions.
Note
I developed this code back in February-March 2019. I just never found the time to sit down and write about it.
Finding the roots
Finding the \(n\) roots of a complex number \(z\) is a very easy task to do using a loop:
MyFindRoots[z_, n_] := Module[{roots, r, angle},
roots = ConstantArray[0, n];
For[k = 0, k < n, k++, {
r = Abs[z],
angle = Arg[z],
r = r^(1 / n),
roots[[k + 1]] = r * Exp[I * (angle + 2 * Pi * k) / n]
}];
roots
]
As an example, we can find the 5th roots of unity shown in the previous section:
A native alternative to MyFindRoots would be to use the Solve function:
However, this function is slower in the range of \(n\) we would solve the problem for (let me know if you find a centrifuge with 1000 holes):
Needs["GeneralUtilities`"]
f1 = MyFindRoots[1, #] &;
f2 = MyFindRootsNative[1, #] &;
BenchmarkPlot[{f1, f2}, # &, Range[100], "IncludeFits" -> True, TimeConstraint -> 60]
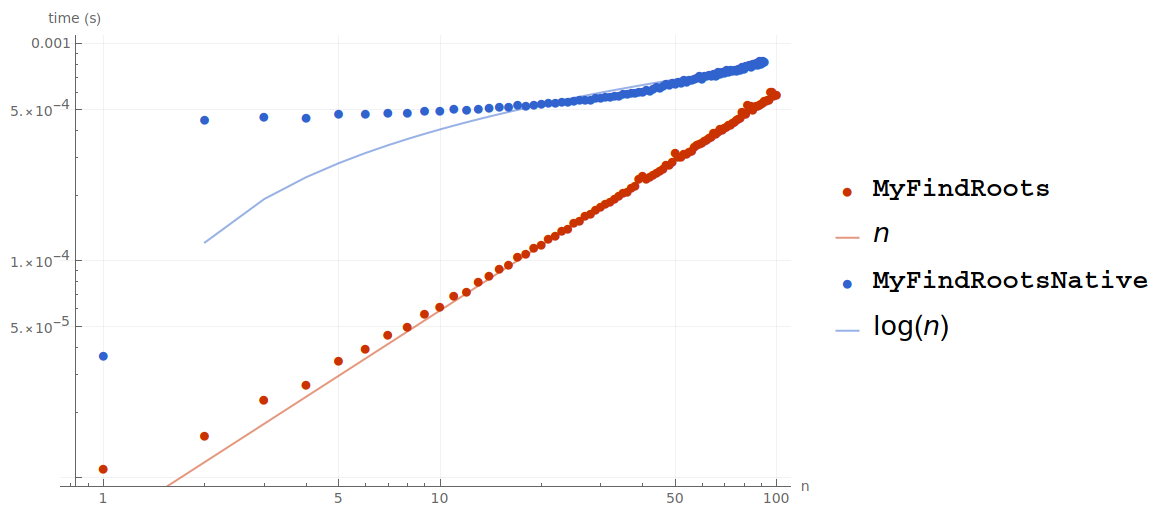
For this reason, we would choose MyFindRoots over the Solve-powered MyFindRootsNative function.
Finding the subsets
One of the awesome things about Mathematica is that operations in set theory are trivial. To get all subset \(S \subseteq R\) we can run, for example,
which results in the list of all possible \(2^{n}\) subsets:
{{}, {1}, {I}, {-1}, {-I}, {1, I}, {1, -1}, {1, -I}, {I, -1}, {I, -I}, {-1, -I}, {1, I, -1}, {1, I, -I}, {1, -1, -I}, {I, -1, -I}, {1, I, -1, -I}}
Checking valid subsets
The problem here will be, thus, checking if the solutions are valid. To calculate the sum of all elements of each subset \(i\) of the family of subsets of \(S\), we can simply do
This example shows that, for \(n=4\), one particular valid solution would be {1, -1}, that is two holes opposite to each other.
Taking all this into account, a simple function to find all possible solutions can be the following:
FindCentrifugeSols[n_] := Module[{solutions, roots, subsets, subset, total, epsilon, i},
roots = UsedFindRoots[1, n];
subsets = Subsets[roots, n];
epsilon = Power[10, -15];
solutions = {};
(*Main loop*)
For[i = 1, i <= Length[subsets], i++, {
subset = subsets[[i]],
total = Total[subset],
If[Abs[N[total]] < epsilon,
solutions = Append[solutions, subset]
]
}];
(*Return*)
{roots, solutions}
]
Let's see it action (note that it returns the set of roots \(R\), and family of valid subsets \(S\)):
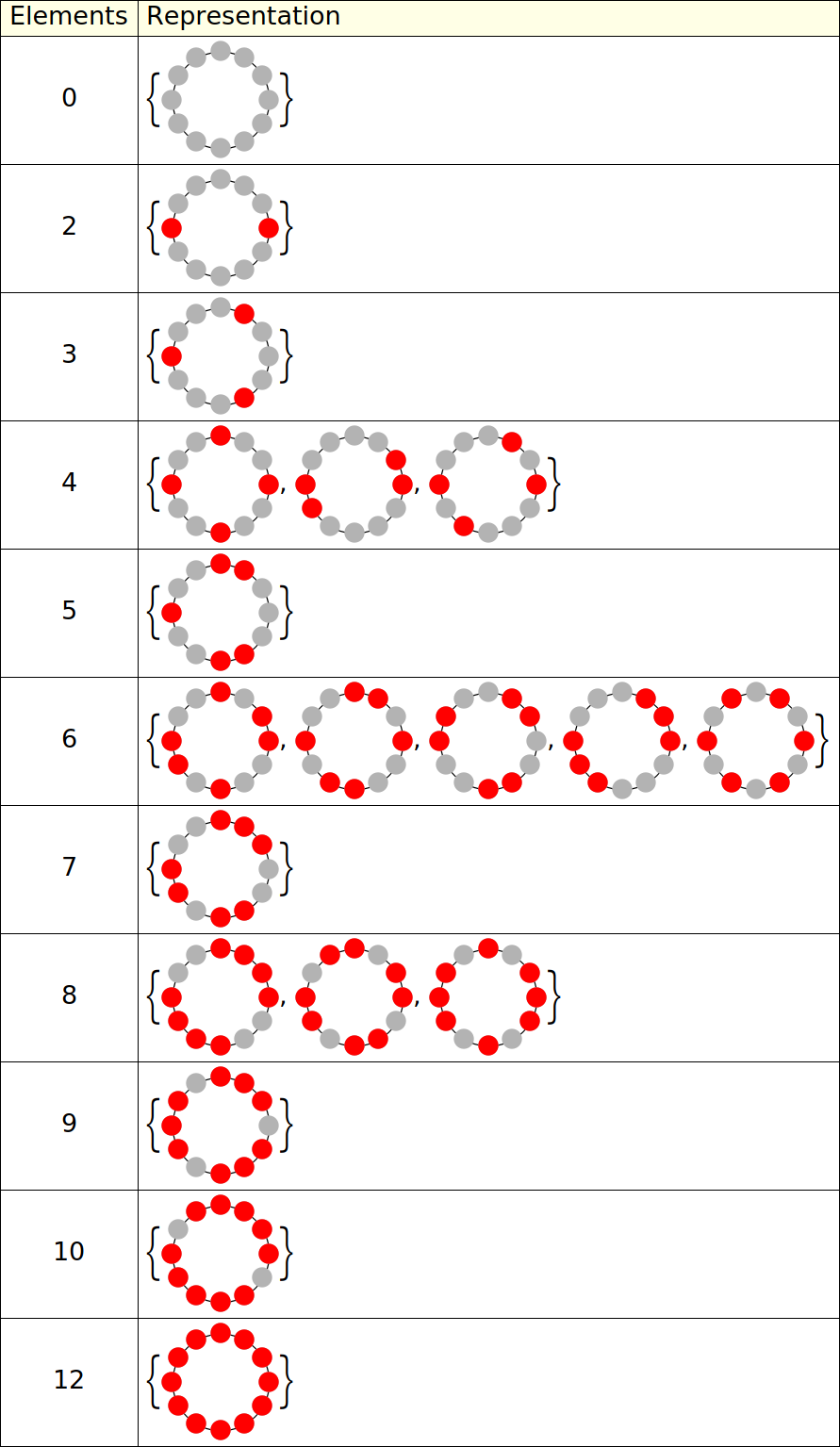
To better visualise the solutions, I wrote a function1 to draw the centrifuge configurations:
An obvious thing to notice here is that for \(k = 2\), the two found solutions are not unique under rotation. This may not seem like a big deal, but for larger values of \(n\), the solution space is littered with non-unique solutions under rotation:
Here's where things get a bit more complicated.
Reducing the solutions
Up to this point, we've already solved the Centrifuge Problem. However, we want to reduce the solutions to truly unique configurations of a centrifuge.
The gist of this step is that we need to rotate all solutions and compare them to each other to get rid of duplicated ones. To accomplish this, we will introduce a set of auxiliary functions:
RotateSol.SortSetClockwise.ClassifyCentrifugeSols.
This function simply applies a rotation of \((2 \pi k)/n\) to a complex number. This is essential to reduce the found solutions to unique solutions under rotations. Notice that this \(k\) is not the amount of test tubes.
SortSetClockwise[set_] := Module[{angles, order},
angles = Map[Arg, set];
order = Ordering[angles, All, NumericalOrder];
angles = angles[[order]];
Map[Exp, I * Pi * Rationalize[N[angles] / Pi]]
]
This step is probably the most important one to minimise calculations. Since we'll be comparing solutions in set form as a whole, we need to make sure they follow a specific, deterministic structure.
ClassifyCentrifugeSols[n_] := Module[{MyMat, MyVect, roots, subsets, subset, epsilon, solutions, curr, next, i},
solutions = FindCentrifugeSols[n];
subsets = Sort[solutions[[2]]];
roots = solutions[[1]];
epsilon = Power[10, -15];
MyMat = {};
MyVect = {};
(*Main loop*)
For[i = 1, i <= Length[subsets], i++, {
subset = subsets[[i]],
curr = Length[subset];
(*Check length of next element*)
If[i + 1 <= Length[subsets],
next = Length[subsets[[i + 1]]],
next = 0
];
(*Append subset to vector*)
MyVect = Append[MyVect, SortSetClockwise[subset]];
(*Append subsets to matrix*)
If[next != Length[subset] && Length[MyVect] > 0,
MyMat = Append[MyMat, {curr, MyVect}];
MyVect = {};
];
}];
(*Return*)
{roots, MyMat}
]
The purpose of this step is to classify solutions by \(k\) (that is, by the amount of test tubes). This is important to make sure at no point we compare {-\(i\), 1, \(i\), -1} with {1, -1}.
If we put all of this together, we can write the following function:
ReduceCentrifugeSols[n_] := Module[{Sols, SubSols, UniqueSubSols, UniqueSols, MyLength, permuteSolsBool, RotatedSol, RotatedSols, Sol, Add, element, i},
Sols = ClassifyCentrifugeSols[n];
MyLength = Length[Sols[[2]]];
UniqueSols = {};
(*Iterate over each subset size*)
For[i = 1, i <= MyLength, i++,
UniqueSubSols = {};
SubSols = Sols[[2]][[i]][[2]];
(*Loop over solution sub-space*)
For[element = 1, element <= Length[SubSols], element++,
RotatedSols = {};
Sol = SubSols[[element]];
Sol = SortSetClockwise[Sol];
(*Rotate one solution*)
For[k = 0, k < n, k++,
RotatedSol = RotateSol[n, k, Sol];
RotatedSol = SortSetClockwise[RotatedSol];
RotatedSols = Append[RotatedSols, RotatedSol]
];
(*Add to list of unique solutions*)
If[Length[Intersection[UniqueSubSols, RotatedSols]] == 0,
UniqueSubSols = Append[UniqueSubSols, Sol];
]
];
UniqueSols = Append[UniqueSols, {Sols[[2]][[i]][[1]], UniqueSubSols}];
];
(*Return*)
{Sols[[1]], UniqueSols}
]
Likewise, I wrote DrawCentrifugeUniqueSols to draw the solutions to ReduceCentrifugeSols:
As we can see, this step of reducing solutions by rotating and comparing them to each other removed {\(i\), \(-i\)} as a duplicate of {1, -1} for \(n = 4\), \(k = 2\).
This improvement becomes super clear when we solve for \(n = 12\), as we go from 100 solutions to only 19:
Going further
Improvement A
One minor issue I've noticed with my ReduceCentrifugeSols method is that it doesn't reduce solutions that are the same under reflections (for instance, \(n = 12\) has actually 18 truly unique solutions, as two of them for \(k = 6\) are the same). This is an issue I may address in the future, but for now I'm happy with my method.
Improvement B
Another point I'd like to work on in the future is to rewrite the code to use pipes (RightComposition), so that functions can be properly composed:
or
Improvement C
Another issue with this method is that the computation time scales exponentially as \(n\) grows. I think by imposing the following condition:
A solution is valid if and only if both the number of test tubes, \(k\), and the number of empty spots, \(n - k\), can be expressed as sums of prime factors of \(n\)
we would be able to remove the step of checking totals, \(\sum s_{i} = 0\), altogether.
-
The full code can be found on https://github.com/aldomann/the-centrifuge-problem/. ↩